Quote of the day - Occam's Razor

Finally, in some areas at least, Nature seems to show an inexplicable simplicity. This is a brute fact, more or less of a bonus, which if it had not existed could not have been expected. As a result, the working scientist learns as a matter of routine experience that he should have faith that the more beautiful and more simple of two equally (inaccurate) theories will end up being a more accurate describer of wider experience. 

This bit of luck vouchsafed the theorist should not be pushed too far, for the gods punish the greedy.

- Paul Samuelson (Theory and Realism: A Reply)

The problem with economic school-ism

Economists are a tribal bunch. The endless list of denominations, schools and sub-schools would be enough to make a Christian theologian blush.

Unfortunately, and while certain irreconcilable differences cannot be denied, there are far too many manufactured controversies that serve only to perpetuate a false sense of "exceptionalism" among various schools of thought. I've written about this kind of thing before, but yesterday a number of blog posts brought the issue to the fore. For instance, here is the indispensable David Glasner arguing persuasively that -- contrary to some dissenting opinions -- Hayek was first and foremost an economist in the neoclassical tradition.

I'd like to briefly focus on a different post written by John Aziz, however, which has also received a fair bit of attention for critiquing the methodology of Ludwig von Mises and Murray Rothbard. I largely agree with what he writes, but was struck by the following introduction:

I am to some extent an Austrian, on three counts. 

First, I subscribe to the notion that value is subjective; that goods’ and services’ values differ according to different individuals because they serve various uses to various users, and that value is entirely in the eye of the beholder. 

Second, I subscribe to the notion that free markets succeed because of the sensitive price feedback mechanism that allocates resources according to the real underlying shape of supply and demand and conversely the successful long-term allocation of labour, capital and resources by a central planner is impossible (or extremely unlikely), because of the lack of a market feedback mechanism.

Third, I subscribe to the notion that human thought is neither linear nor rational, and the sphere of human behaviour is complicated and multi-dimensional, and that attempts to model it using linear, mechanistic methods will in the long run tend to fail.

This really puzzled me. I sincerely wonder how anyone could regard the first two points as uniquely -- or even especially -- Austrian.[*] Subjective valuation and role of the price mechanism are fundamental concepts to virtually every school of economic thought, and certainly those found within the mainstream corpus. It's true that matters are complicated by the consideration of (say) externalities, but if these qualities are characteristic of Austrians... well, then basically all of us would qualify.

In fact, subjective value didn't even originate as an "Austrian" concept. The idea can be formally traced back to Jules Dupuit at least, a French engineer from the early 19th century who also expressed a keen interest in economics. Ironically, he developed his ideas on subjective utility in response to Jean Baptiste Say -- an otherwise revered figure in Austrian circles -- who had described utility as the objective worth of a good. Similarly, the role of the price mechanism and the impossibility (quote unquote) of central planning was also not entirely original to Mises and Hayek, but a "reprise of earlier Pareto-Barone-Wieser-Taylor debates". Now of course if must be pointed out that, for example, Friedrich von Wieser was a founder of the eponymous Austrian school, but you could convincingly make the case that the key role of prices had been well established long before that...

At this point, I don't wish to be too unkind to John. I enjoyed his post and judging by his response to me in the comments section, he was mostly trying to strike a conciliatory tone before moving on to his criticisms. However, this sort of thing is far too prevalent in the economic debates that I find myself in, with heterodox schools being especially guilty... and I say that as someone with strong sympathies for a number of heterodox positions. Unfortunately, despite a number of valid criticisms against the mainstream, many supporters of heterodox economics continue to demonstrate a very poor understanding of the fact that many of “their” ideas are actively embraced and shared by the rest of the profession. (Nick Rowe is another person recently given to exasperation after dealing with one too many lazy jibes from armchair critics, although in this case I can think of at least one person who is holding firm.) 

THOUGHT FOR THE DAY: Denying the impact that your favourite thinkers have had on other economists is a strange way to honour their legacy.

___

[*] I'd say there's a case to be made for the third point as well, but it is a more complex topic requiring nuanced discussion so we'll leave it aside for the moment.

Is gold highly correlated with money supply?

Amidst all this talk about US Republicans eyeing a return to the gold standard, something on my twitter feed earlier this week caught the eye: A link to an old Zero Hedge post together with a claim that "there is a 93% correlation between M2 [money supply] and gold". A similar post here is more specific in saying "[t]he correlation between the total U.S. M2 and gold has exceeded 0.90 since November 2004".

Now presumably, this tweet was aimed at countering the inconvenient fact that the correlation between price inflation (i.e. CPI) and gold is virtually zero. And, if predictions of imminent hyperinflation have yet to materialise, well then at least "hard money" types can point to way in which monetary inflation has manifesting itself in the surging gold price of the last decade. (There's a lesson to be learned here about the velocity of money, kids, but that will have to wait until another time...)

Anyway here's a graph of the gold price and U.S. M2 since 2004, taken from the FRED website. Both are shown in terms of moving monthly averages and, sure enough, the correlation looks very high indeed.



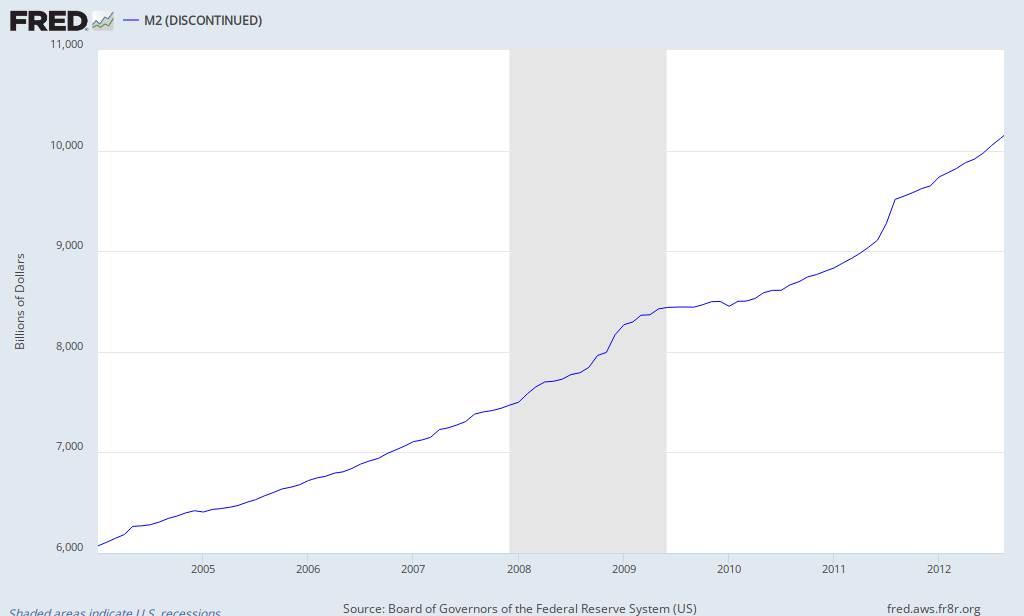
Unfortunately, there are two things wrong with this picture. The first is that the time-frame really does matter. The second has to do with the statistical properties of these series. Let's take these two issues in turn.

Consider what happens when we look at the period from 1981 (which is first date for which FRED has data on both series) until 2004.



Woah! That positive relationship isn't looking too good all of a sudden. Now, of course, I can already hear angry golden-tinged voices accusing me of dueling a strawman. The correlation coefficient was specifically cited for the 2004-post period, so who really cares about what happened 20 or 30 years ago? Okay, perhaps something special happened around the mid-2000s that explains why the two variables have since become so intertwined. Fine, but then don't try to tell me that it's anything specifically to do with money supply. The noticeable kink in the M2 series leading up to that moment occurs around 1995 (after a period of mild tapering), which is close on a decade before the supposed special relationship with gold prices begins.

The broader point here is that if you are going posit a structural theory for why two variables are related, then that relationship needs to have enduring qualities. If not, how can you be sure that gold and M2, rather than one causing the other, aren't both being driven by some other factor? (For one thing, the money supply is supposed to be endogenous to what is happening in the broader economy...) I'm inclined to argue that focusing on the period since 2004 is just a form of data-mining and, as we'll see next, not a particularly good example of that anyway.

Okay. So, ignore the fact that the (weak) longer-term correlation between M2 and gold prices matters. Surely, eight years of data showing a 90%+ correlation can't be denied? Surely, we can say with extreme confidence that recent gold prices have been greatly influenced by money supply? Right?

RIGHT??

Sadly, no. Whenever someone points excitedly to very high correlations between trending time-series, your spidey-sense should be going off like Peter Parker on methylamphetamine. The reason lies with one of the fundamental concepts in time-series econometrics: Nonstationarity.

Wait a minute. Are those series... nonstationary?

Without getting too bogged down by statistical concepts, nonstationary series are characterized by a mean and variance that are changing over time. It's not that they can't be growing or declining over time, but rather that they should consistently return to some kind of mean trend. The most important thing from our perspective is failing to account for this issue will generally lead to spurious (i.e. "nonsense") regression results; an idea that goes all the way back to a classic paper by Yule  in 1926.

Aaaaaaaand.... as you might have guessed by now, the above series are nonstationary. In technical parlance, they are referred to as random walks with drift. Now, there is a famous exception to this rule that occurs when two series are said to be "cointegrated". Again, I'd rather avoid delving too deeply into the murky waters of statistics in a blog post, but suffice to say that that cointegration does not hold here.

To avoid the problems of bullshit spurious regressions, we must therefore adopt a tried and tested approach: Take the first differences of the series and only then test for correlation. Doing so produces a correlation coefficient of exactly <drum roll>... 0.32. Moreover, if we actually regress gold on M2 we get a pretty unimpressive R-squared statistic of 0.1. In other words, only ten percent of the gold's movements are explained by what is happening to money supply.  [UPDATE: Based on the comments, let me again emphasise that these numbers are specifically for the "highly" correlated post-2004 period.]

THOUGHT FOR THE DAY: Simply regressing gold prices on any nonstationary series -- whether that be iPhone sales or the number of Crocs™ wearers in Bangladesh -- would likely produce equally impressive, but obviously bogus, results. Now gold fans might be inclined to protest loudly at this point: "Duh", but there's no theoretical basis for linking those goods to gold. We have a theory that predicts the price of gold will rise with (monetary) inflation!" Except that we've just tested that theory and found it, if not entirely wanting, then at least highly oversold. Perhaps a bit like gold then... [See comments.]

PS - For anyone interested in checking all of this for themselves, here is some Stata code that I used to test the series. The code will always call the most recently available FRED data, so the exact figures you get may differ from those presented here depending on when you run it.

NOTE: In writing this post, I see that others have effectively made the same point before.